if(!require(devtools)) install.packages("devtools")## Loading required package: devtools## Warning: package 'devtools' was built under R version 3.3.3library(nltsa)library(astsa) # load astsa package
sunspot = sqrt(sunspot.year) # transform sunspot data
plot(sunspot, xlab="year") # plot data 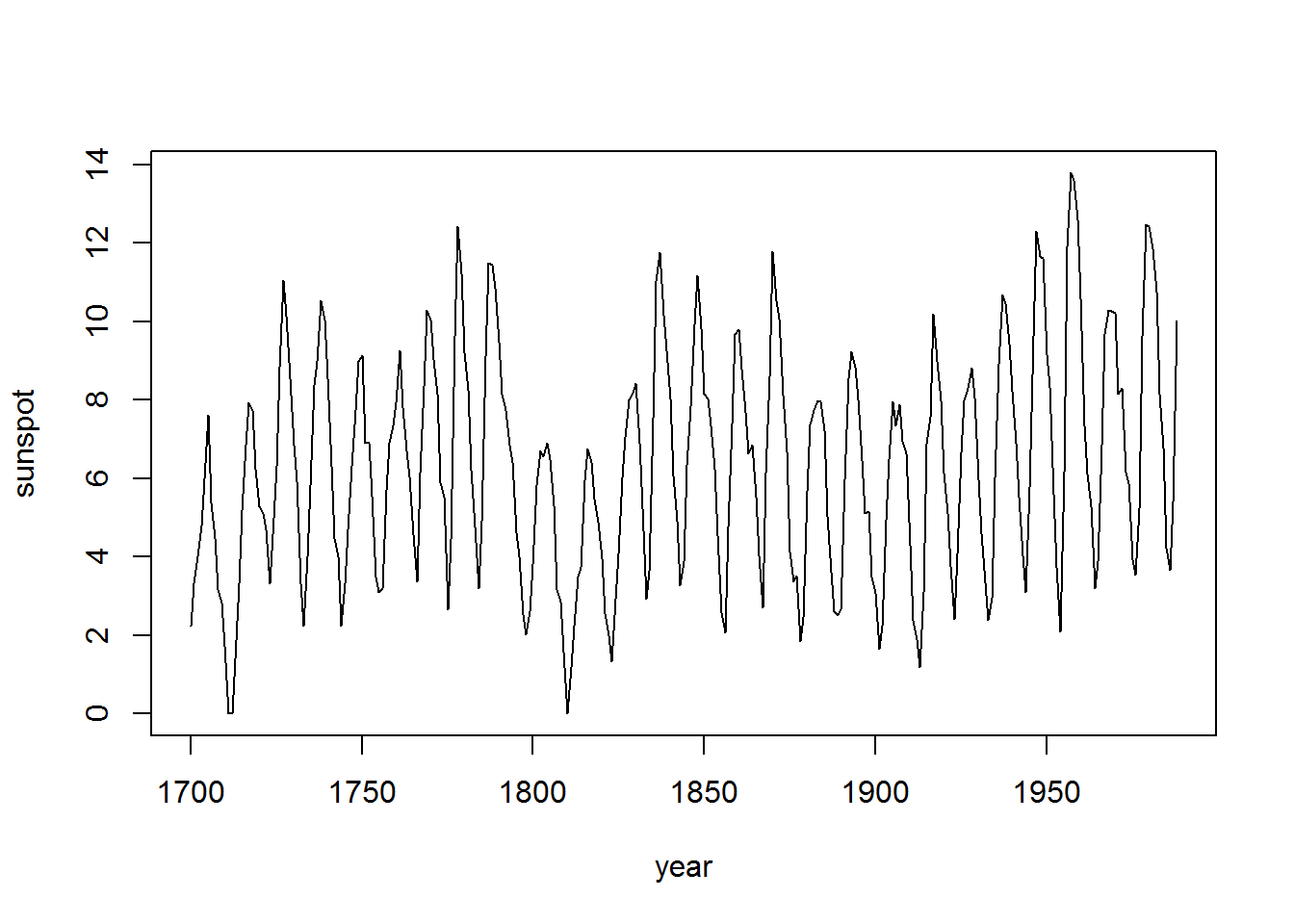
acf2(sunspot) # not shown 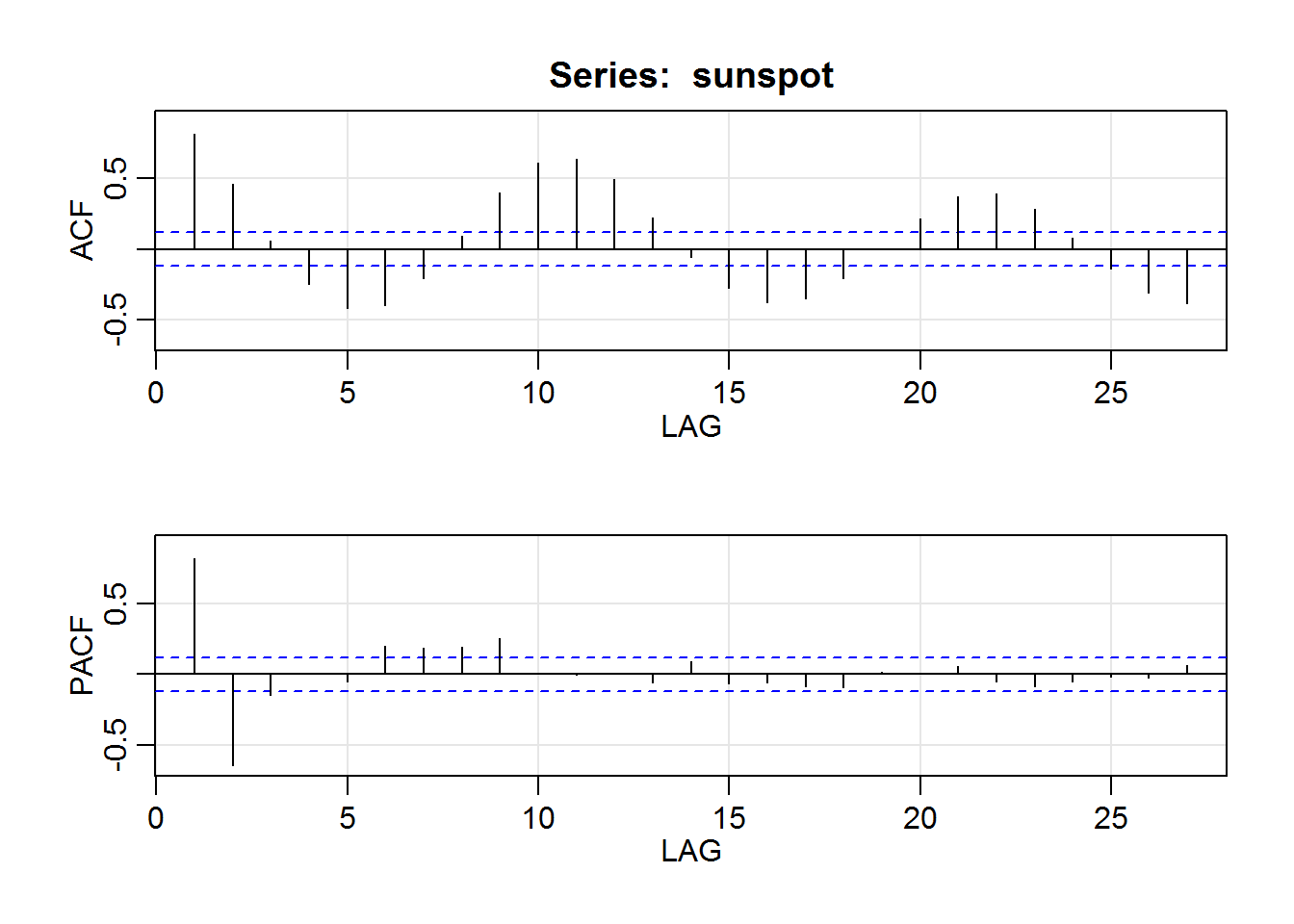
## ACF PACF
## [1,] 0.82 0.82
## [2,] 0.46 -0.65
## [3,] 0.06 -0.15
## [4,] -0.25 0.01
## [5,] -0.42 -0.05
## [6,] -0.40 0.20
## [7,] -0.20 0.18
## [8,] 0.09 0.19
## [9,] 0.40 0.25
## [10,] 0.61 0.01
## [11,] 0.64 0.00
## [12,] 0.49 0.00
## [13,] 0.23 -0.06
## [14,] -0.06 0.09
## [15,] -0.27 -0.06
## [16,] -0.38 -0.06
## [17,] -0.35 -0.09
## [18,] -0.21 -0.09
## [19,] 0.00 0.02
## [20,] 0.22 0.00
## [21,] 0.37 0.06
## [22,] 0.40 -0.05
## [23,] 0.29 -0.09
## [24,] 0.08 -0.05
## [25,] -0.14 -0.02
## [26,] -0.31 -0.03
## [27,] -0.38 0.06ar(sunspot) # uses AIC to find the best fit with Yule-Walker estimates ##
## Call:
## ar(x = sunspot)
##
## Coefficients:
## 1 2 3 4 5 6 7 8
## 1.1471 -0.3914 -0.1454 0.2021 -0.2255 0.0791 0.0514 -0.1104
## 9
## 0.2514
##
## Order selected 9 sigma^2 estimated as 1.346arima(sunspot, order=c(9,0,0)) # final model fit via MLE ##
## Call:
## arima(x = sunspot, order = c(9, 0, 0))
##
## Coefficients:
## ar1 ar2 ar3 ar4 ar5 ar6 ar7 ar8
## 1.2194 -0.4792 -0.1423 0.2695 -0.2432 0.0173 0.1679 -0.2057
## s.e. 0.0565 0.0906 0.0943 0.0948 0.0954 0.0959 0.0962 0.0921
## ar9 intercept
## 0.2972 6.4018
## s.e. 0.0573 0.5798
##
## sigma^2 estimated as 1.084: log likelihood = -423.92, aic = 869.84sunspot = sqrt(sunspot.year) # if you didn't save it from previous example
sun.ar = spec.ar(sunspot, plot=FALSE) # parametric
sun.np = spectrum(sunspot, spans=c(5,5), plot=FALSE) # nonparametric
plot(sun.ar$freq, sun.ar$spec, type="l", log="y", ylab="spectrum", xlab="frequency")
lines(sun.np$freq, sun.np$spec, lty=2)
legend("topright", c("parametric","nonparametric"), lty=1:2) 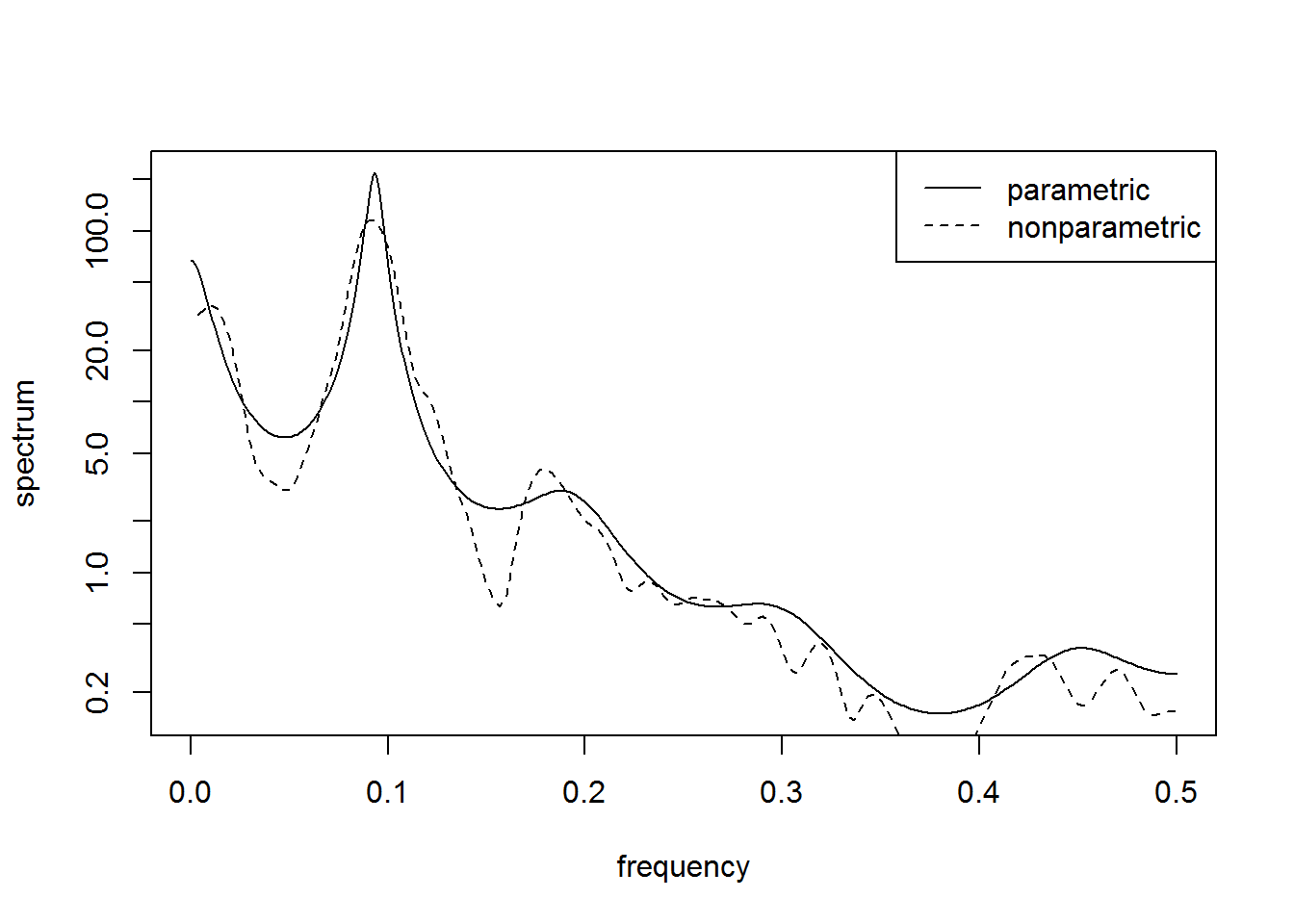
Chapter 2 examples:
library(astsa)
# Generate data
set.seed(1)
num = 10
w = rnorm(num+1)
v = rnorm(num)
mu = cumsum(w) # states
y = mu[-1] + v # observations
# Smooth
mu0 = 0; sigma0 = 1; phi = 1; cQ = 1; cR = 1
(ks = Ksmooth0(num, y, 1, mu0, sigma0, phi, cQ, cR))## $xs
## , , 1
##
## [,1]
## [1,] -0.447615
##
## , , 2
##
## [,1]
## [1,] -1.06607
##
## , , 3
##
## [,1]
## [1,] -0.8509158
##
## , , 4
##
## [,1]
## [1,] 0.4111808
##
## , , 5
##
## [,1]
## [1,] 0.3131779
##
## , , 6
##
## [,1]
## [1,] 0.7474054
##
## , , 7
##
## [,1]
## [1,] 1.631918
##
## , , 8
##
## [,1]
## [1,] 2.152879
##
## , , 9
##
## [,1]
## [1,] 2.37808
##
## , , 10
##
## [,1]
## [1,] 3.065433
##
##
## $Ps
## , , 1
##
## [,1]
## [1,] 0.472136
##
## , , 2
##
## [,1]
## [1,] 0.4508498
##
## , , 3
##
## [,1]
## [1,] 0.4477443
##
## , , 4
##
## [,1]
## [1,] 0.4472926
##
## , , 5
##
## [,1]
## [1,] 0.4472362
##
## , , 6
##
## [,1]
## [1,] 0.4472926
##
## , , 7
##
## [,1]
## [1,] 0.4477443
##
## , , 8
##
## [,1]
## [1,] 0.4508498
##
## , , 9
##
## [,1]
## [1,] 0.472136
##
## , , 10
##
## [,1]
## [1,] 0.618034
##
##
## $x0n
## [,1]
## [1,] -0.2238075
##
## $P0n
## [,1]
## [1,] 0.618034
##
## $J0
## [,1]
## [1,] 0.5
##
## $J
## , , 1
##
## [,1]
## [1,] 0.4
##
## , , 2
##
## [,1]
## [1,] 0.3846154
##
## , , 3
##
## [,1]
## [1,] 0.3823529
##
## , , 4
##
## [,1]
## [1,] 0.3820225
##
## , , 5
##
## [,1]
## [1,] 0.3819742
##
## , , 6
##
## [,1]
## [1,] 0.3819672
##
## , , 7
##
## [,1]
## [1,] 0.3819662
##
## , , 8
##
## [,1]
## [1,] 0.381966
##
## , , 9
##
## [,1]
## [1,] 0.381966
##
## , , 10
##
## [,1]
## [1,] NA
##
##
## $xp
## , , 1
##
## [,1]
## [1,] 0
##
## , , 2
##
## [,1]
## [1,] -0.0353115
##
## , , 3
##
## [,1]
## [1,] -1.200542
##
## , , 4
##
## [,1]
## [1,] -1.632214
##
## , , 5
##
## [,1]
## [1,] 0.4717644
##
## , , 6
##
## [,1]
## [1,] 0.04480118
##
## , , 7
##
## [,1]
## [1,] 0.2007435
##
## , , 8
##
## [,1]
## [1,] 1.309947
##
## , , 9
##
## [,1]
## [1,] 2.013696
##
## , , 10
##
## [,1]
## [1,] 1.953273
##
##
## $Pp
## , , 1
##
## [,1]
## [1,] 2
##
## , , 2
##
## [,1]
## [1,] 1.666667
##
## , , 3
##
## [,1]
## [1,] 1.625
##
## , , 4
##
## [,1]
## [1,] 1.619048
##
## , , 5
##
## [,1]
## [1,] 1.618182
##
## , , 6
##
## [,1]
## [1,] 1.618056
##
## , , 7
##
## [,1]
## [1,] 1.618037
##
## , , 8
##
## [,1]
## [1,] 1.618034
##
## , , 9
##
## [,1]
## [1,] 1.618034
##
## , , 10
##
## [,1]
## [1,] 1.618034
##
##
## $xf
## , , 1
##
## [,1]
## [1,] -0.0353115
##
## , , 2
##
## [,1]
## [1,] -1.200542
##
## , , 3
##
## [,1]
## [1,] -1.632214
##
## , , 4
##
## [,1]
## [1,] 0.4717644
##
## , , 5
##
## [,1]
## [1,] 0.04480118
##
## , , 6
##
## [,1]
## [1,] 0.2007435
##
## , , 7
##
## [,1]
## [1,] 1.309947
##
## , , 8
##
## [,1]
## [1,] 2.013696
##
## , , 9
##
## [,1]
## [1,] 1.953273
##
## , , 10
##
## [,1]
## [1,] 3.065433
##
##
## $Pf
## , , 1
##
## [,1]
## [1,] 0.6666667
##
## , , 2
##
## [,1]
## [1,] 0.625
##
## , , 3
##
## [,1]
## [1,] 0.6190476
##
## , , 4
##
## [,1]
## [1,] 0.6181818
##
## , , 5
##
## [,1]
## [1,] 0.6180556
##
## , , 6
##
## [,1]
## [1,] 0.6180371
##
## , , 7
##
## [,1]
## [1,] 0.6180344
##
## , , 8
##
## [,1]
## [1,] 0.6180341
##
## , , 9
##
## [,1]
## [1,] 0.618034
##
## , , 10
##
## [,1]
## [1,] 0.618034
##
##
## $like
## [,1]
## [1,] 9.433598
##
## $Kn
## [,1]
## [1,] 0.618034# Plot smoother
plot.ts(mu[-1], type="p", ylim=c(-3,5), main="Smoother")
lines(ks$xs)
lines(ks$xs+2*sqrt(ks$Ps), lty=2, col=4)
lines(ks$xs-2*sqrt(ks$Ps), lty=2, col=4)
library(astsa)
# Generate Data
set.seed(999); num = 100
x = arima.sim(n=num+1, list(ar = .8, sd=1))
y = ts(x[-1] + rnorm(num,0,1))
init.par = c(phi=.1, sigw=1, sigv=1) # initial parameters
# Function to evaluate the likelihood
Linn = function(para){
phi = para[1]; sigw = para[2]; sigv = para[3]
Sigma0 = (sigw^2)/(1-phi^2); Sigma0[Sigma0<0]=0
kf = Kfilter0(num, y, 1, mu0=0, Sigma0, phi, sigw, sigv)
return(kf$like)
}
# Estimation
(est = optim(init.par,Linn,gr=NULL,method="BFGS",hessian=TRUE,control=list(trace=1,REPORT=1)))## initial value 103.600205
## iter 2 value 89.479862
## iter 3 value 82.246403
## iter 4 value 81.867027
## iter 5 value 79.256645
## iter 6 value 79.092247
## iter 7 value 79.018099
## iter 8 value 79.015258
## iter 9 value 79.014778
## iter 10 value 79.014721
## iter 11 value 79.014673
## iter 12 value 79.014484
## iter 13 value 79.014452
## iter 13 value 79.014452
## iter 13 value 79.014452
## final value 79.014452
## converged## $par
## phi sigw sigv
## 0.8137667 0.8507704 0.8744035
##
## $value
## [1] 79.01445
##
## $counts
## function gradient
## 37 13
##
## $convergence
## [1] 0
##
## $message
## NULL
##
## $hessian
## phi sigw sigv
## phi 253.370612 67.39986 -9.640648
## sigw 67.399856 78.99260 48.611452
## sigv -9.640648 48.61145 92.206339SE = sqrt(diag(solve(est$hessian)))
cbind(estimate=c(est$par[1],est$par[2],est$par[3]), SE) ## estimate SE
## phi 0.8137667 0.08060501
## sigw 0.8507704 0.17528644
## sigv 0.8744035 0.14293017library(astsa)
library(nlme)
# Generate data (same as previous example)
set.seed(999); num = 100
x = arima.sim(n=num+1, list(ar = .8, sd=1))
y = ts(x[-1] + rnorm(num,0,1))
# EM procedure - output not shown
(em = EM0(num, y, 1, mu0=0, Sigma0=2, Phi=.1, cQ=1, cR=1, 75, .00001))## iteration -loglikelihood
## 1 103.5944
## 2 89.35611
## 3 82.23511
## 4 79.54581
## 5 78.62453
## 6 78.28685
## 7 78.15941
## 8 78.10651
## 9 78.08045
## 10 78.06495
## 11 78.05428
## 12 78.04627
## 13 78.03994
## 14 78.03479
## 15 78.03051
## 16 78.0269
## 17 78.02382
## 18 78.02116
## 19 78.01884
## 20 78.01681
## 21 78.01502
## 22 78.01342
## 23 78.01199
## 24 78.01071
## 25 78.00955
## 26 78.00849
## 27 78.00753
## 28 78.00665
## 29 78.00584
## 30 78.00509## $Phi
## [,1]
## [1,] 0.7990194
##
## $Q
## [,1]
## [1,] 0.7667703
##
## $R
## [,1]
## [1,] 0.7169766
##
## $mu0
## [,1]
## [1,] -2.40108
##
## $Sigma0
## [,1]
## [1,] 0.07665366
##
## $like
## [1] 103.59439 89.35611 82.23511 79.54581 78.62453 78.28685 78.15941
## [8] 78.10651 78.08045 78.06495 78.05428 78.04627 78.03994 78.03479
## [15] 78.03051 78.02690 78.02382 78.02116 78.01884 78.01681 78.01502
## [22] 78.01342 78.01199 78.01071 78.00955 78.00849 78.00753 78.00665
## [29] 78.00584 78.00509
##
## $niter
## [1] 30
##
## $cvg
## [1] 9.582724e-06# Standard Errors (this uses nlme)
mu0 = em$mu0; Sigma0 = em$Sigma0
para = c(em$Phi, sqrt(em$Q), sqrt(em$R))
# evaluate likelihood at estimates
Linn = function(para){
kf = Kfilter0(num, y, 1, mu0, Sigma0, para[1], para[2], para[3])
return(kf$like)
}
# get SEs
emhess = fdHess(para, function(para) Linn(para))
SE = sqrt(diag(solve(emhess$Hessian)))
# Display Summary of Estimation
estimate = c(para, em$mu0, em$Sigma0); SE = c(SE, NA, NA)
u = cbind(estimate, SE)
rownames(u) = c("phi","sigw","sigv","mu0","Sigma0"); u## estimate SE
## phi 0.79901942 0.07915803
## sigw 0.87565420 0.16321525
## sigv 0.84674472 0.13792771
## mu0 -2.40107981 NA
## Sigma0 0.07665366 NAlibrary(astsa)
set.seed(123)
num = 50
w = rnorm(num,0,.1)
x = cumsum(cumsum(w)) # states
y = x + rnorm(num,0,1) # observations
plot.ts(x, ylab="", lwd=2, ylim=c(-1,8))
lines(y, type='o', col='#808080')
# the model (specified by the parameters)
Phi = matrix(c(2,1,-1,0),2)
A = matrix(c(1,0),1)
mu0 = matrix(c(0,0),2)
Sigma0 = diag(c(1,1))
# innovations likelihood
Linn = function(para){
sigw = para[1]; sigv = para[2]; cQ = diag(c(sigw,0))
kf = Kfilter0(num,y,A,mu0,Sigma0,Phi,cQ,sigv)
return(kf$like)
}
# estimation
init.par = c(.1,1)
(est = optim(init.par, Linn, NULL, method="BFGS", hessian=TRUE)) ## $par
## [1] 0.0816401 0.9385482
##
## $value
## [1] 33.47605
##
## $counts
## function gradient
## 27 7
##
## $convergence
## [1] 0
##
## $message
## NULL
##
## $hessian
## [,1] [,2]
## [1,] 557.49454 69.45007
## [2,] 69.45007 94.43305(SE = sqrt(diag(solve(est$hessian)))) ## [1] 0.04443707 0.10797015# smooth and add to plot
sigw = est$par[1] # = 0.08 (se: 0.04)
cQ = diag(c(sigw,0))
sigv = est$par[2] # = 0.94 (se: 0.11)
ks = Ksmooth0(num,y,A,mu0,Sigma0,Phi,cQ,sigv)
xsmoo = ts(ks$xs[1,1,]); psmoo = ts(ks$Ps[1,1,])
upp = xsmoo+2*sqrt(psmoo)
low = xsmoo-2*sqrt(psmoo)
lines(xsmoo, col=4, lty=2, lwd=3)
lines(upp, col=4, lty=2)
lines(low, col=4, lty=2)
# fit spline and add to plot
lines(smooth.spline(y), lty=1, col=2)
# add legends
legend("topleft", c("Observations","State"), pch=c(1,-1), lty=1, lwd=1:2, col=c('#808080',1))
legend("bottomright", c("Smoother", "GCV Spline"), lty=c(2,1), lwd=c(3,1), col=c(4,2) )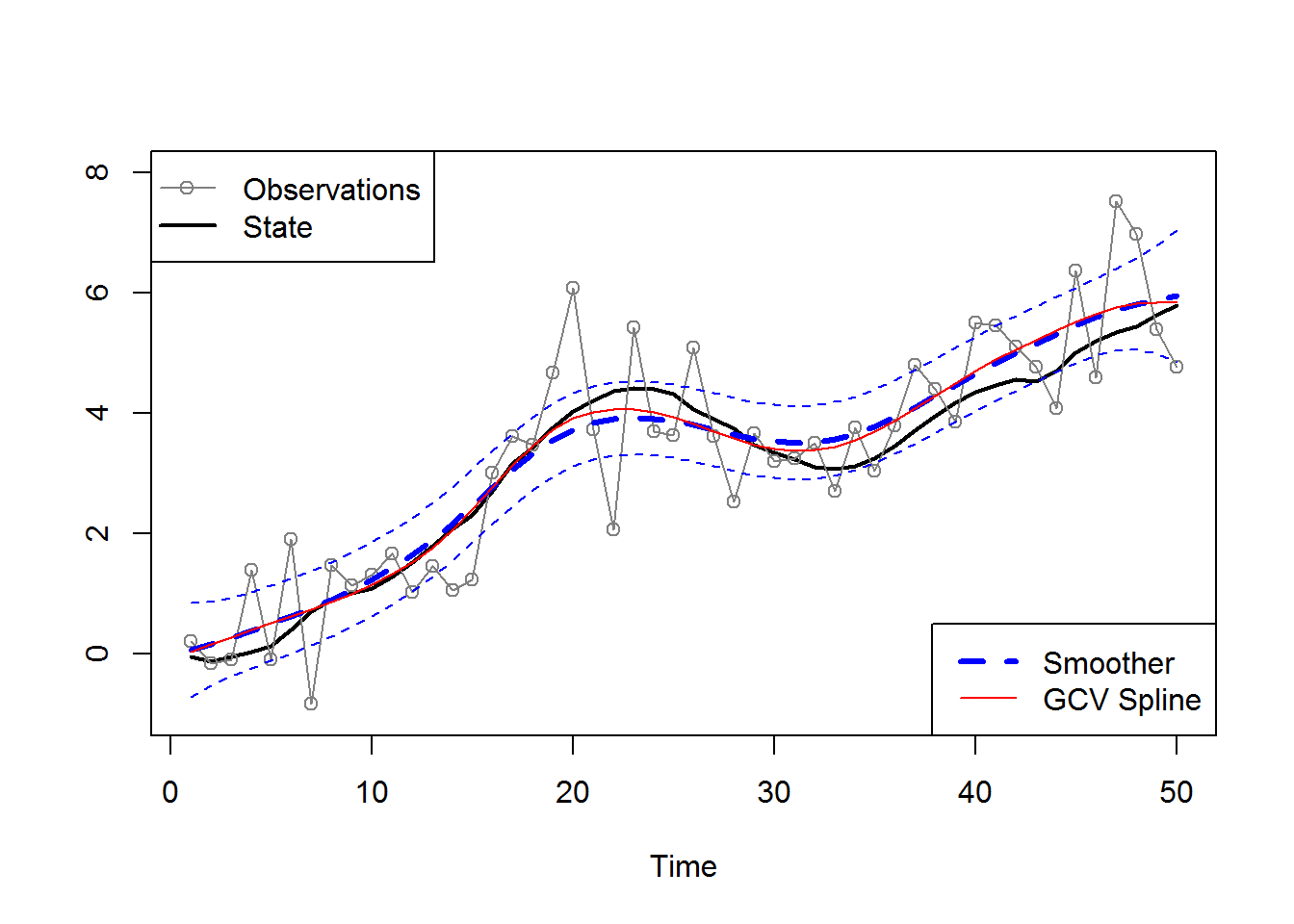
Reference: Nonlinear Time Series Theory, Methods and Applications with R Examples: by Randal Douc, Eric Moulines

Share this post
Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email